Путем замены переменной Р в передаточной функции ФНЧ на переменную (1/ΔΩ)(P+1/P) можно получить АЧХ полосового фильтра. В результате этого преобразования АЧХ фильтра нижних частот в диапазоне 0 ≤ Ω ≤ 1 переходит в правую часть полосы пропускания полосового фильтра (1 ≤ Ω ≤ ΩMAX). Левая часть полосы пропускания является зеркальным отображением в логарифмическом масштабе правой части относительно средней частоты полосового фильтра Ω = 1 (рис. 2.36). При этом ΩMIN = 1/ ΩMAX. Вычисление 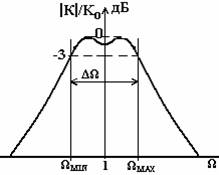 нормированных частот среза полосового фильтра, на которых его коэффициент передачи уменьшается на 3 дБ, может быть осуществлено из
нормированных частот среза полосового фильтра, на которых его коэффициент передачи уменьшается на 3 дБ, может быть осуществлено из
![]() . (2.79)
. (2.79)
формулы которая получается при
![]() и
и ![]()
Рис. 2.36
Передаточная функция ПФ второго порядка имеет вид
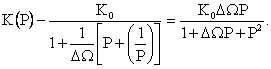 (2.80)
(2.80) Основными характеристиками такого фильтра являются коэффициент передачи КР на резонансной частоте (КР = К0) и добротность Q.
Из (2.82) получим выражения для АЧХ и ФЧХ полосового фильтра второго порядка
 (2.83)
(2.83)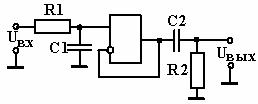
Получить полосовой фильтр можно, включив последовательно фильтры нижних и верхних частот (рис. 2.37). Максимальная величина добротности, которая может быть получена, при таком построении фильтра равна Q= 1/2.
Рис. 2.37
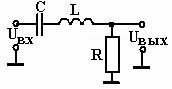
На рис. 2.38 показана схема пассивного LRC – фильтра. Передаточная функция равна
![]() . (2.84)
. (2.84)
Резонансная частота фильтра ![]() .
.
Передаточная функция (2.84) может быть переписана в
Рис. 2.38 нормированном виде
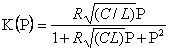 . (2.85)
. (2.85)
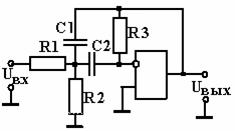
Для реализации пассивного полосового фильтра с низкой резонансной частотой требуется большая индуктивность. Для схемной реализации можно использовать операционный усилитель с частотно-зависимой обратной RC – связью. Пример ПФ со сложной отрицательной обратной связью показан на рис. 2.39. Приняв С1 = С2 = С получим передаточную функцию в виде
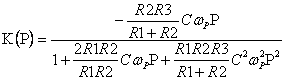 . (2.86)
. (2.86)
Рис. 2.39 Согласно (2.82) имеем
Отсюда получим, что
Подставив (2.88) в (2.86) получим и приравняв соответствующие коэффициенты к коэффициентам в формуле (2.82) можно получить, что
Полоса пропускания
Таким образом, полоса пропускания не зависит от R1 и R2, а КР не зависит от R2. Поэтому можно изменять резонансную частоту fР, изменяя R2 без изменения коэффициента передачи КР.
Рассмотрим пример расчета полосового фильтра. Пусть необходимо получить ПФ с резонансной частотой fР = 10 Гц, добротностью Q= 100 и коэффициентом передачи на резонансной частоте КР = -10. При этом частоты среза будут fMIN ≈ 9,95 Гц и fР ≈ 10,05 Гц. Задаем произвольно значение емкости конденсатора С = 1 мкФ. Тогда из формул (2.89) получим R3 = Q/(πfPC) = 3,18 МОм; R1= R3/(-2KP) =159 кОм. Из формулы (2.88) получим
R2= -KР/(2Q2 + KР)= 79,5 Ом.
На рис. 2.40 приведен пример схемы полосового фильтра с положительной обратной связью.
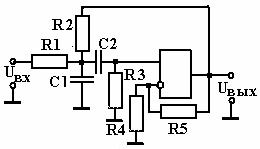
Рис. 2. 40