Исследование сигналов может
осуществляться не только во временной, но и частотной (спектральной) областях.
Приборы предназначенные для
экспериментального анализа спектра, называются анализаторами спектра. В
основе спектральных методов анализа
лежит преобразование Фурье.
Периодическую
функцию можно представить рядом Фурье в виде
![]() , (8.1)
, (8.1)
где
![]() - амплитудный спектр (спектр амплитуд);
- амплитудный спектр (спектр амплитуд);
![]() - фазовый спектр.
- фазовый спектр.
Для
представления непериодических функций используют формулу интеграла Фурье:
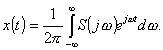 (8.2)
(8.2)
Величину S (jω) называют
комплексным спектром непериодической функции. Комплексный спектр можно вычислить по прямому
преобразованию Фурье:
![]() (8.3)
(8.3)
Из
(8.3) получим выражения для
амплитудного S(ω) и фазового
φ(ω) спектров непериодического сигнала, которые могут быть
представлены в виде
![]() ;
;
![]() , (8.4)
, (8.4)
где 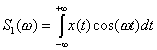 ;
; 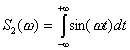 .
.
Выражение (8.4)
показывает, что для получения спектра необходимо бесконечное время анализа.
Аппаратурный анализ спектра, как правило, ограничен во времени и поэтому
получить истинный спектр сигнала невозможно. Аппаратурно можно получить текущий
спектр сигнала
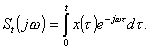 (8.5)
(8.5)
При большом времени анализа текущий спектр может быть достаточно хорошим приближением к истинному спектру.
При построении
анализаторов спектра можно
использовать выражение
(8.5) в чистом
виде, т. е. произвести все математические
операции над сигналом согласно выражению
(8.5). Этот тип анализаторов используется
достаточно широко в связи
с развитием цифровой вычислительной
техники. Однако наиболее распространены анализаторы
спектра с использованием резонаторов.
Простейшим резонатором является
колебательный контур,
изображенный на рис. 8.1.
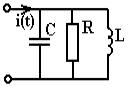
Рис. 8.1.
Основные характеристики
контура следующие: d=Ω/ω0 = √ L/C/R - затухание; ω0=√1/LC—собственная частота;
Q= 1/d—добротность; Ω = ω0/Q — полоса пропускания (на уровне 0,707).
Более сложные
резонаторы могут содержать ряд усилителей или других активных
элементов.
Анализаторы
спектра в зависимости от метода и способа проведения анализа спектра
разделяются на: 1) фильтровые; 2) дисперсионные; 3) рециркуляционные; 4)
цифровые.
По способу проведения анализа
спектра различают параллельные, последовательные, комбинированные анализаторы спектра.
Анализаторы параллельного
типа содержат набор резонаторов, каждый из которых настроен на
определенную частоту анализируемого диапазона частот. При таком способе анализа
нет потерь информации в реальном масштабе времени, и он эффективен как для
периодических, так и непериодических сигналов. Недостатком подобных
анализаторов является их сложность и большие аппаратные затраты.
В
анализаторах спектра последовательного типа собственная частота
резонатора медленно (по сравнению с сигналом) изменяется во всем,
анализируемом, диапазоне частот. Составляющие спектра выделяются и
анализируются последовательно
(поочередно). Такой анализ эффективен только для периодических и
квазипериодических сигналов (по сравнению с временем анализа), а также
стационарных случайных сигналов. Анализаторы последовательного действия проще в
аппаратном отношении по сравнению с параллельными анализаторами.
В комбинированных анализаторах сочетаются преимущества параллельного и
последовательного способов анализа.
8.1.1. Характеристики анализаторов спектра.
8.1.2. Фильтровые анализаторы спектра.