Аналоговые измерительные устройства

          Одной  из  основных причин возникновения погрешности является отклонение  температуры  от  градуировочной (температурная погрешность). При повышении температуры уменьшаются магнитная индукция в рабочем зазоре (индукция уменьшается примерно на 0,2 % на 10 ⁰С) и удельный противодействующий момент (удельный противодействующий момент уменьшается примерно на 0,2-0,4 % на 10 ⁰С), увеличивается электрическое сопротивление обмотки рамки и токоподводов (пружинок или растяжек).

          Следует отметить, что при уменьшении магнитной индукции показания магнитоэлектрического прибора уменьшаются, а при уменьшении удельного противодействующего момента показания увеличиваются. Таким образом, эти два фактора взаимно компенсируют друг друга.

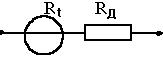
Рис. 3.7.

Для уменьшения температурной погрешности, обусловленной изменением электрического сопротивления обмотки рамки и растяжек (или пружинок), в магнитоэлектрических   приборах   применяются   различные схемные решения (рис. 3.7).  Эту погрешность  можно  уменьшить,  вклю­чая последовательно с температурно-зависимым сопротивлением R_t  добавочное сопротивление R_Д из материала, электрическое   сопротивление  которого  практически  не зависит от температуры Результирующий температурный коэффициент такой цепи

,                 (3.9)

где α_R – результирующий  температурный  коэффициент  сопротивления цепи; α_R - температурный  коэффициент  сопротивления материала рамки.

Из выражения (3.9) видно, что чем больше может быть отношение R_Д/R_t, тем меньше α_R  и, следовательно, тем меньше температурная погрешность γ_t. Для вольтметров на пределы измерения больше 3—5В можно уменьшить γ_t до значений, соответствующих классу точности 0,2 и даже 0,1. Для милливольтметров, к которым можно отнести и амперметры с шунтом, этот способ компенсации неэффективен, прежде всего, потому, что связан с увеличением собственного потребления, т. е. с уменьшением чувствительности прибора.

Для милливольтметров основными схемами температурной компенсации являются последовательно-параллельная схема (рис.3.8,а) и схе­ма с термосопротивлением (рис. 3.8,б).   

                                                                                 

                     а)                                                               б)

          Рис.3.8.

Электрическая цепь измерительного механизма состоит из сопротивления обмотки R₀ и последо­вательно с ним включенного сопротив­ления упругих элементов (пружинок или растяжек) R₁. Температурные коэффициен­ты электрического сопротивления мате­риалов обмотки  и упругих элементов, как правило, различны. При расчете сопротивление упругих элементов раз­бивают на две части: «медную»,  имеющую  температурный  коэффициент  такой  же, как и материал обмотки, выполняемой обычно из меди, и «манганиновую» - с  нулевым температурным коэффициентом. На схеме рис. 3.8 обозначены: R₀ – сумма сопротивлений обмотки и «медной» части упругих элементов (α₀); R₁ – сумма «манганиновой» части сопротивления упругих элементов и добавочного  сопротивления  из манганина  (α₁  = 0);  R₂ – добавочное  сопротивление из манганина (α₂ = 0); R₃ – сопротивление шунта, выполняемого обычно из меди или никеля (α₃).

Температурная погрешность находится как:

,   (3.10)

где I₀ – ток в цепи ИМ при температуре градуировки t₀; I_{0 t}  ток в цепи ИМ при температуре t = t + θ;

.                       (3.11)

          Вторая составляющая в выражении (2.10) много меньше первой и ей можно пренебречь. В этом случае температурная погрешность γ_t будет равна нулю, если выполняется условие

.                        (3.12)

Из (3.12) следует, что  условие,  при  котором  выполняется  требование  γ_t = 0, не содержит температуру перегрева θ, т. е. справедливо для любого диапазона изменения температур. Такой вывод имеет место в результате принятого допущения (исключе­нием из рассмотрения зависимости γ_t от составляющей, содержа­щей θ²). Учет этой зависимости показывает, что в действитель­ности для заданного диапазона изменения температуры θ тре­бование γ_t = 0 можно выполнить только для двух температур внутри этого диапазона.

Рассмотренная схема обладает вы­сокой   стабильностью,   технологично­стью и позволяет обеспечить требуе­мую температурную компенсацию для приборов самых высоких классов точ­ности, имеет большое собственное потребление. От этого недостатка свободна схема с полупроводниковым терморезистором  (рис.3.8,б).  Однако  ввиду недостаточно высокой воспроизводимости свойств и пониженной стабильности схемы с терморезисторами применяют только в приборах классов точности 1,5; 2,5 и не выше чем класса 0,5. Применяют другие схемы и методы термокомпенсации — мостовые схемы,  термомагнитные шунты  и т. д.